Démonstration de la formule mathématique utilisée pour le placement à versements périodiques.
Préalable : la suite géométrique
La suite suivante présente une progression où chaque terme est le terme précédent multiplié par deux.
Suite = 10 + 20 + 40 + 80 + 160 + 320 + ...
Chaque terme peut être exprimé sous la forme 10 × 2n avec 'n' la position du terme dans la suite (en partant de zéro).
On appelle cette suite une suite géométrique de premier terme 10 et de raison 2. La somme des 'n' premiers éléments de cette suite est donnée par la formule suivante :
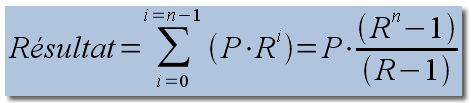
Ainsi, si on calcule la suite donnée en introduction sur les 6 premiers termes (10 + 20 + 40 + 80 + 160 + 320), on obtient : Résultat = 10 × (26-1) / (2-1) = 630.
La formule est valable pour une raison différente de 1. Dans le cas particulier d'une raison égale à 1, il faut appliquer la formule suivante :
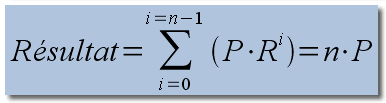
Pour trouver d'autres informations sur les suites, recherchez sur internet dans un moteur de recherche progression ou suite géométrique. De nombreuses pages existent, notamment les sites des universités. A l'origine de cette page, nous avons utilisé des informations en provenance de Apprendre-en-ligne.net.
Les puissances
Petit rappel sur les propriétés des puissances :
a0 = 1
a1 = a
a2 = a × a
an = a × a × ... × a
a-1 = 1 / a
a-2 = 1 / (a × a)
a-n = 1 / (a × ... × a)
am × an = am+n
am / an = am-n
Placement à versement régulier
Bon, venons-en à notre placement.
On va prendre un placement à 4% de 100 € chaque 1er janvier pendant 4 ans.
Le premier versement va devenir 100 x 1,04 x 1,04 x 1,04 x 1,04 ; le deuxième : 100 x 1,04 x 1,04 x 1,04, ... La valeur de l'ensemble du placement va être de 100 × 1,044 + 100 × 1,043 + 100 × 1,042 + 100 × 1,041.
Cela ressemble presque à une suite géométrique de premier terme 100 et de raison 1,04. Il manque le terme de rang 0, soit 100 x 1,040 ou simplement 100.
Autrement dit , le résultat est égal à la somme des 5 premiers termes d'une suite géométrique de premier terme 100 et de raison 1,04, à laquelle il faut ôter 100.
Soit le résultat = [100 x (1,045 - 1) / (1,04 - 1)] - 100
En remplaçant la raison par (1 + taux) ; le nombre de termes par le nombre d'années (ou plus généralement de périodes), on aboutit à la formule suivante :
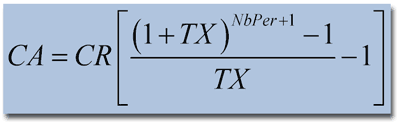
CA : le total du capital acquis à la fin du placement, CR : le montant de chaque versement, TX : le taux d'intérêts de la période, NbPer : le nombre de périodes ou nombre de versements.
© MoneyVox 2005-2024 / Droits réservés